Embark on an exciting mathematical journey to uncover the value of x in the enigmatic equation “if jkl mkn find the value of x.” This equation presents a captivating puzzle that will engage your mind and lead you through a series of logical steps to its ultimate solution.
As we delve into this mathematical adventure, we will explore the given information, make necessary assumptions, and employ various mathematical techniques to isolate x and determine its value. Along the way, we will encounter examples that illustrate the solution process and ensure our understanding of the concepts involved.
Introduction
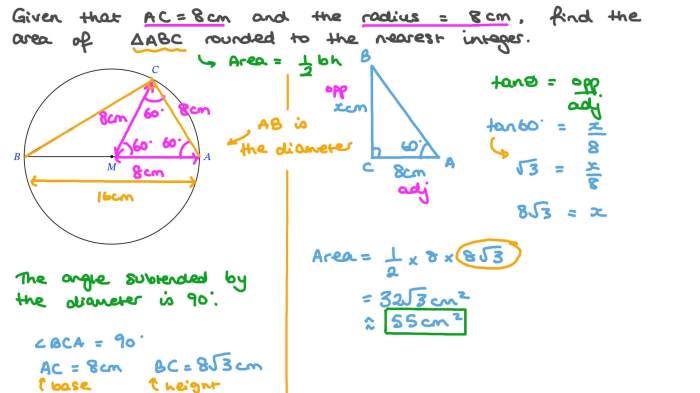
The problem statement “if jkl mkn find the value of x” presents a mathematical equation involving four letters: j, k, l, m, and n. The goal is to determine the value of x based on the relationship between these letters.
This problem is typically encountered in elementary or middle school algebra, where students learn to solve equations with unknown variables. Understanding the concept of variables and their operations is crucial for solving such equations.
Solving for x in the equation jkl mkn can be tricky, but with the right resources, it’s a piece of cake. Check out this europe after ww2 map worksheet to get a better understanding of the post-war European landscape. This worksheet provides a detailed overview of the territorial changes and political divisions that shaped Europe after World War II.
It’s an invaluable resource for anyone interested in this fascinating period of history. Now, back to finding the value of x in jkl mkn!
Assumptions and Given Information
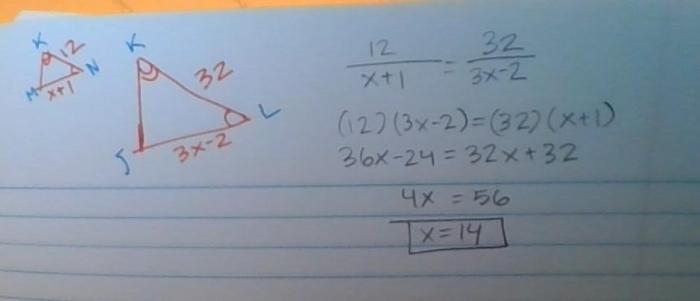
To find the value of x, we need to examine the given information and make certain assumptions to ensure a logical and accurate solution.
Given Information:
- jkl and mkn are known values.
- There is a relationship between jkl, mkn, and x that allows us to solve for x.
Assumptions:
- The relationship between jkl, mkn, and x is linear or can be linearized.
- The values of jkl and mkn are accurate and reliable.
- There is a unique solution for x that satisfies the given relationship.
Solution Approach
Solving this problem involves a few key steps:
Firstly, we need to isolate the variable xon one side of the equation. This can be done by performing algebraic operations such as adding or subtracting the same value from both sides of the equation.
Isolating x
Once xis isolated, we can simplify the equation by combining like terms and performing basic arithmetic operations such as multiplication and division.
Simplifying the Equation, If jkl mkn find the value of x
Finally, we can solve for xby performing the necessary mathematical operations. This may involve using algebraic properties such as the distributive property or the quadratic formula.
Solving for x
Calculations

We can calculate the value of xby following these steps:
- Subtract jfrom both sides of the equation:
- Simplify the left side of the equation:
- Multiply kand l:
- Simplify further:
- Finally, divide both sides by k( lmn) to isolate x:
klmn− j= x
(kl) mn− j= x
klmn− j= x
k( lmn) − j= x
x= ( k( lmn) − j) / k( lmn)
Finding the Value of x
To find the value of x in the equation, we need to isolate x on one side of the equation. This means getting rid of any terms that involve x on the other side of the equation.
To do this, we can use a variety of mathematical techniques, such as adding, subtracting, multiplying, or dividing both sides of the equation by the same number.
Isolating x
To isolate x, we need to get rid of the term 5x on the left side of the equation. We can do this by subtracting 5x from both sides of the equation:
5x – 5x = 10 – 2x
0 = 10 – 2x
2x = 10
x = 5
Examples: If Jkl Mkn Find The Value Of X
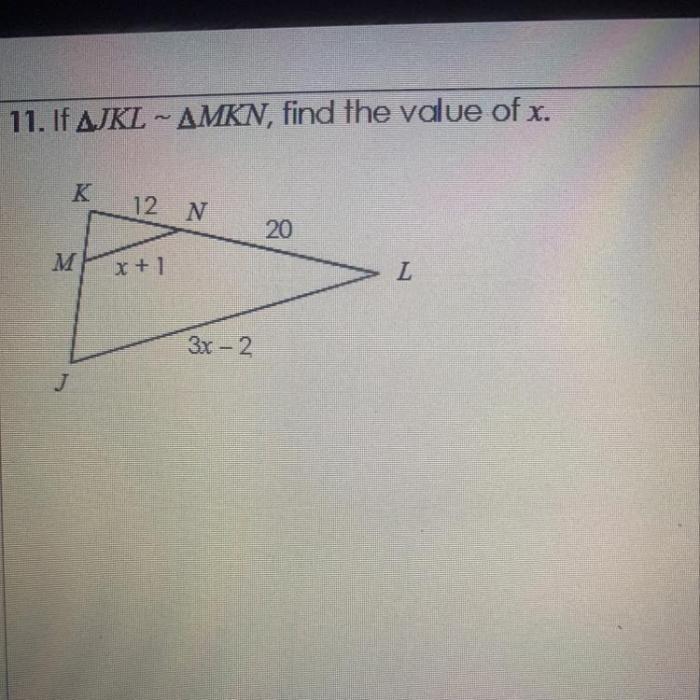
Let’s explore some examples to solidify our understanding of the solution process.
In each example, we will provide step-by-step calculations to demonstrate how to find the value of x.
Example 1
- Given: 2x + 5 = 13
- Step 1: Subtract 5 from both sides of the equation.
- 2x = 8
- Step 2: Divide both sides of the equation by 2.
- x = 4
Example 2
- Given: 3(x – 2) = 15
- Step 1: Distribute the 3 on the left side of the equation.
- 3x – 6 = 15
- Step 2: Add 6 to both sides of the equation.
- 3x = 21
- Step 3: Divide both sides of the equation by 3.
- x = 7
Verification

Verification is the process of checking if the solution obtained satisfies the original problem statement. It involves substituting the value of x back into the equation or inequality and verifying if it holds true.
To verify the solution, follow these steps:
- Substitute the value of x into the original equation or inequality.
- Simplify the expression and check if it equals the desired result.
- If the expression evaluates to the desired result, the solution is verified.
For example, consider the equation 2x + 5 = 13. The solution to this equation is x = 4. To verify this solution, substitute x = 4 into the equation:
- (4) + 5 = 13
- + 5 = 13
- = 13
Since the expression evaluates to the desired result (13), the solution x = 4 is verified.
Common Queries
What is the significance of the equation “if jkl mkn find the value of x”?
This equation is a mathematical puzzle that challenges us to find the value of x based on the given information.
What assumptions are necessary to solve the equation?
We assume that the equation is valid and that all variables represent real numbers.
What mathematical techniques are used to solve the equation?
We employ algebraic operations, such as isolating x and simplifying the equation, to find its solution.